注:本人的运行环境:macOS-10.13.4, Python-3.6, Tensorflow-1.4.1
bp基本公式原理
基本公式原理主要分为三块:
* bp正向传播子过程
* bp反向传播子过程
* 输出层到隐藏层更新策略
* 隐藏层到隐藏层的更新策略
于是分三块来计算。
bp正向传播子过程

很简单,对于某个节点,假设就是OutputLayer的第j个节点,它的输出值,是由【前一层所有的节点的输出值】+【前一层所有节点与该节点相连的权值$w_{ij}$】+【该节点的偏置$b_j$】+【激励函数F(x)】,这四个部分组成。
具体公式很简单,就一个$Y_j$表示该节点输出,$X_i$表示上一层第i个节点的输出,w表示权值,b表示偏置,F表示激励函数:
\[Y_j = F(\sum_{i=0}{w_{ij}*X_{ij}} + b_j)\]这个没什么好说的,了解基本原理即可知道,毕竟就是全连接的矩阵运算而已,重点是反向传播。
bp反向传播,输出层->隐藏层更新策略
首先定义Loss函数记为E,$Y_j$表示输出层第j个点输出值,$S_j$表示真实标签值:
\[E = \frac{1}{2} * \sum_{j=0}{(S_j-Y_j)^2}\]然后根据这个Loss的值调整w和b,所以要计算两者的梯度,先计算w的梯度:
\[\Delta w_{ij} = -\alpha \frac{\partial E}{\partial w_{ij}}\]为什么是负,我们要沿着梯度相反的方向,然后我们要做的,就是把E的值带进去,进行换算:
\[\Delta w_{ij} = -\alpha \frac{\partial \frac{1}{2} * \sum_{j=0}{(S_j-Y_j)^2} }{\partial w_{ij}}\] \[\Delta w_{ij} = -\alpha \sum_{j=0}{S_j-Y_j}*\frac{\partial (S_j-Y_j)}{\partial w_{ij}}\]$S_j$是个常数,对w求偏导为0,所以消掉:
\[\Delta w_{ij} = +\alpha \sum_{j=0}{S_j-Y_j}*\frac{\partial (Y_j)}{\partial w_{ij}}\]$Y_j$按照正向传播子过程的公式代入,整合:
\[\Delta w_{ij} = +\alpha \sum_{j=0}{S_j-Y_j} *\frac{\partial (F( \sum_{i=0}{w_{ij}*X_{ij}} + b_j))}{\partial w_{ij}}\]可以看到F是一个关于w的函数,那么对w求偏导,我们假设一般情况下激励函数F这样表示:
\[F(x) = \frac{A}{1 + e^{\frac{-x}{B}}}\]则 $F’(x) = \frac{1}{AB} f(x)(A - f(x))$,把这个式子带进上面的梯度表达式继续化简:
\[\Delta w_{ij} = +\alpha \sum_{j=0}{(S_j-Y_j)*Y_j*(1-Y_j)}*\sum_{i=0}{X_i}\]把前面关于j的式子都提出来,为什么?因为前面都是关于$S_j$和$Y_j$的式子,说白了,就是【误差】,令$\delta_{ij}$等于这个【误差】:
\[\delta_{ij} = \sum_{j=0}{(S_j-Y_j)*Y_j*(1-Y_j)}\]那么最后就化简完成了:
\[\Delta w_{ij} = \alpha * \delta_{ij} * (\sum_{i=0}{X_i})\]有了梯度的式子,那么更新策略就是沿着梯度反向走呗:
\[w_{ij} = w_{ij} - \Delta w_{ij}\]同理,b也一样:
\[b_{j} = b_{j} - a*\delta_{ij}\]bp反向传播,隐藏层->隐藏层更新策略
它和上面那个最大的区别就是:【要利用后一层已经得到的$\delta$】
推导过程和上面完全一样,j是输出层第j个点,i是靠近输出层的隐含层的第i个点,k是和隐含层相连的那个隐含层的第k个点,我们已经有$\delta_{ij}$了,要求计算$\delta_{ki}$
梯度算出来还是一样的,由$\delta_{ki}$和自己这一层所有输出的和:
\[\Delta w_{ki} = \beta * \delta_{ki} *\sum_{k=0}{x_k}\]其中:
\[\delta_{ki} = \delta_{ij} * (\sum_{k=0}{w_{kj}})*Y_i*(1-Y_i)\]更新策略即为:
\[w_{ki} = w_{ki} - \beta * \delta_{ki} * \sum_{k=0}{x_k}\] \[b_{i} = b_{i} - \beta * \delta_{ki}\]总结
bp计算过程看上去多(公式打的我手都算了),然而其实就三(一大堆)个公式:
正向传播子过程:$Y_j = F(\sum_{i=0}{w_{ij}*X_{ij}} + b_j)$
输出层反向隐藏层更新参数策略:
\[w_{ij} = w_{ij} - \alpha * \delta_{ij} * (\sum_{i=0}{X_i})\] \[b_{j} = b_{j} - a*\delta_{ij}\]其中
\[\delta_{ij} = \sum_{j=0}{(S_j-Y_j)*Y_j*(1-Y_j)}\]隐藏层反向更新隐藏层参数策略:
\[w_{ki} = w_{ki} - \beta * \delta_{ki} * \sum_{k=0}{x_k}\] \[b_{i} = b_{i} - \beta * \delta_{ki}\]其中
\[\delta_{ki} = \delta_{ij} * \sum_{k=0}{w_{kj}}*Y_i*(1-Y_i)\]当然,这些公式推导都是来源于loss函数和激励函数,拿准他们,你就可以推导出来上面这一堆了:
\[E = \frac{1}{2} * \sum_{j=0}{(S_j-Y_j)^2}\] \[F(x) = \frac{A}{1 + e^{\frac{-x}{B}}}\]深度学习基本概念细节
这里随便记录一些基本的东西,然后给出一些参考的解答,作为防备面试题用233.
主要内容是:
- 过拟合问题
- L1,L2正则
- 数据增强
- Dropout
- 梯度消失问题
- loss函数的相关细节
过拟合问题
原来的Loss Function还记得么,在本系列第四篇教程里,Loss Function后面是带了一个尾巴的。
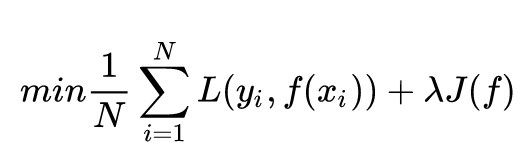
后面的尾巴就是正则,表示在原本的损失上,要带上使用参数本身所带来的损耗。过拟合本身就是因为激活神经元太多了嘛,试想如果参数不带损耗,那就为所欲为了,被激活的节点哪怕只有一点也会激活,而如果加上了损耗,它的值的变化没有覆盖掉参数带的损失,那么就不会被激活了。
L1正则
\[L_1 = \sum_{i=1}^{k}{\|\|w_i\|\|_1}\]w表示参数,k表示参数的个数,说白了就是所有参数的和。
L2正则
\[L_1 = \sum_{i=1}^{k}{(\|\|w_i\|\|_2)^2}\]在L1的基础上变成了平方。
L1正则更容易得到稀疏解也就是抑制神经元。
Dropout
这个就是单纯的强行抑制一部分神经元让它不激活。单纯让神经元的输出乘了某个随机数。
可以参考这一篇:https://yq.aliyun.com/articles/68901
梯度消失问题
这一篇讲的够好了:https://www.cnblogs.com/tsiangleo/p/6151560.html
什么是梯度消失?前面隐藏层学习速度远远低于后面隐藏层。
产生原因?sigmoid本身特性导致。
解决方法?使用ReLU。
loss函数相关细节
除了之前的那种loss,还有很多现在比较流行的。
比如当初学nlp的时候看《数学之美》,里面引入了信息熵的概念,然后Cross-Entropy交叉熵作为一种loss现在天天都出现在视野中,还有MSE,K-L散度等。
当然,这篇文章讲得够好了,各种细节和比较都说明了,如果想让我单独再写的话给我留言,https://blog.csdn.net/haolexiao/article/details/70142571